Oft wird der Wellenwiderstand eines Kabel als charakteristischer Wert genannt.
Grundsätzlich gilt, daß eine Übertragungsleitung nur bei einem bestimmten Abschlußwiderstand die Energie vollständig und reflexionsfrei übertragen kann. Dieser Abschlußwiderstand muß so groß sein wie der Wellenwiderstand der Leitung.
Bei einem vom Wellenwiderstand abweichenden Abschlußwiderstand der Leitung wird ein Teil der Energie nicht übertragen, sondern reflektiert und es kommt zu sog. stehenden Wellen.
Der Wellenwiderstand bei Leitungen wirkt grundsätzlich für das Verhältnis zwischen Strom und Spannung des Signals wie ein ohmscher Widerstand, ohne daß er allerdings wie dieser einen dissipativen, d.h. energieverbrauchenden Charakter besitzt (wenn man von den ohmschen Anteilen in L und C einmal absieht) und ist daher wie dieser auch frequenzunabhängig.
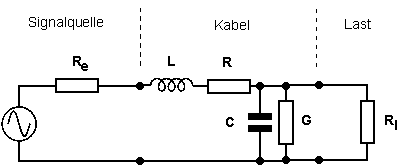
Der Wellenwiderstand ist unabhängig von der Länge der Leitung, hängt in der Hauptsache nur vom mechanischen Aufbau der Leitung ab und berechnet sich bei hohen Frequenzen unter Vernachlässigung der Verluste in erster Näherung
| Z = √(L / C) |
mit
Z = Wellenwiderstand [Ω]
L = Leitungsinduktivität [H]
C = Leitungskapazität [F]
√() = Quadratwurzel
und weiter
| L = µ × µ r × l × (1 + (4 × ln(a / r)))/(4 × π) |
mit
L = Leitungsinduktivität [H]
µ = Permeabilitätskonstante = 4 × p ×10 -7 H/m
µr = relative Permeabilität (bei nichtmagnetischen Stoffen = 1)
l = Leiterlänge [m]
r = Leiterradius [m]
a = Abstand zwischen Hin- und Rückleiter [m]
π = Kreiszahl = 3.1415927
ln = natürlicher Logarithmus
bzw.
| C = p × ε × εr × l/(ln (a / r) |
mit
C = Leitungskapazität [F]
ε = Dielektrizitätskonstante = 8.855 ×10 -12 F/m
er = Dielektrizitäts- oder Permittivitätszahl (Luft = 1)
l = Leiterlänge [m]
r = Leiterradius [m]
a = Abstand zwischen Hin- und Rückleiter [m]
π = Kreiszahl = 3.1415927
ln = natürlicher Logarithmus
Obige Formeln beziehen sich auf nebeneinander liegende Leiter mit kreisförmigem Querschnitt.
In der Praxis kann man (in der Hochfrequenztechnik) die Wellenwiderstände verschiedener Leiterkonfigurationen überschlägig wie folgt bestimmen:
a. symmetrisches Leiterpaar:
mit gleichem Durchmesser d [cm] im Abstand a [cm]
| Z = (60 / √(εr)) × ln ((2a² / d²) - 1 + (2a / d) × √((a² / d²) - 1)) |
mit
Z = Wellenwiderstand [Ω]
er = Dielektrizitäts- oder Permittivitätszahl (Luft = 1)
ln = natürlicher Logarithmus
√() = Quadratwurzel
b. übereinanderliegende Flachbandleitung:
mit Breite b [cm], der Dicke c [cm] im Abstand a [cm]
| Z = (87 / √(εr + 1.4)) × ln(6a / (0.8b + c)) |
c. zwei konzentrisch ineinander liegende kreisförmige Zylinder (Koaxialkabel):
mit innerem Durchmesser d [cm] und äußerem Durchmesser D [cm]
| Z = (60 / √(εr)) × ln(D / d) |
Für sehr tiefe Frequenzen (also z.B. Audiobereich) berechnet sich der Wellenwiderstand annähernd mit
| Z = √(R / (2 × π × f × C)) |
mit
Z = Wellenwiderstand [Ω]
R = Leitungswiderstand [Ω]
C = Leitungskapazität [F]
f = Frequenz [Hz]
π = Kreiszahl = 3.1415927
√() = Quadratwurzel
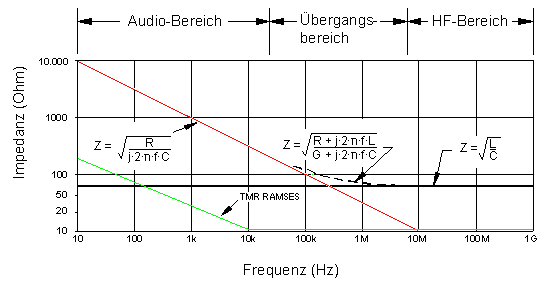
Man sieht, daß hier der Wellenwiderstand bei Audiofrequenzen seine Frequenzunabhängigkeit verliert und aufgrund seiner kapazitiven Komponente mit sinkenden Frequenzen ansteigt.
In der Vergangenheit gab es Versuche, durch Kombination von nachträglicher Impedanzlinearisierung des Lautsprechers und einer Lautsprecherleitung mit einem (Wellen?)Widerstand von 8 Ohm u. U. klangliche Vorteile zu erzielen.
Dies scheiterte vermutlich nicht zuletzt am extrem geringen Wirkungsgrad dieser Kombination. Die klanglichen Ergebnisse waren ebenfalls, aus welchen Gründen auch immer, nicht sehr überzeugend.
Es ist leicht ersichtlich, daß zur Erzielung von sehr niedrigen Wellenwiderständen in der Größenordnung der nominalen Lautsprecherimpedanz mit verhältnismäßig großen Leitungskapazitäten gerechnet werden muß, die hohe Anforderungen an die Stabilität des Endverstärkers bei ungeschickten Konstruktionen stellen.
Die resultierenden Signalausbreitungsgeschwindigkeiten berechnen sich bei sehr hohen Frequenzen wie folgt:
| v = 1 / √(L × C) |
mit
v = Signalgeschwindigkeit [m/s]
L = Leitungsinduktivität [H]
C = Leitungskapazität [F]
√() = Quadratwurzel
bzw. bei nichtmagnetischen Stoffen
| v = c / √(εr) |
mit
v = Signalgeschwindigkeit [m/s]
c = Lichtgeschwindigkeit = 3 × 108 m/s
εr = Dielektrizitäts- oder Permittivitätszahl (Luft = 1) des verwendeten Dielektrikuns
√() = Quadratwurzel
Berücksichtigt man die Verluste (bei niedrigen und mittleren Frequenzen), so ergibt sich folgendes Bild:
| v = 2 × π × f / IM[ √(R + j × 2π × f × L) × (G + j × 2π × f × C)] |
mit
v = Signalgeschwindigkeit [m/s]
f = Frequenz [Hz]
π = Kreiszahl = 3.1415927
IM = Imaginärteil des komplexen Nenners
j = imaginäre Zahl (j2 = -1)
G = dielektrischer Verlustleitwert [1/Ω]
R = Leitungswiderstand [Ω]
C = Leitungskapazität [F]
L = Leitungsinduktivität [H]
√() = Quadratwurzel
Für Signalgemische ergibt sich auf Leitungen, durch frequenzabhängige Verluste bedingt, eine frequenzabhängige Signalausbreitungsgeschwindigkeit (Dispersion).
Zuweilen begegnet man in diesem Zusammenhang dem Begriff "Heaviside-Bedingung".
Diese ist erfüllt, wenn
| G / C = R / L |
mit
G = dielektrischer Verlustleitwert [1/O]
R = Leitungswiderstand [O]
C = Leitungskapazität [F]
L = Leitungsinduktivität [H]
Wenn diese Bedingung erfüllt ist, heben sich die Auswirkungen der Verluste auf und die Signalausbreitungsgeschwindigkeit wird frequenzunabhängig.
Allerdings müssen dazu in der Praxis die dielektrischen Verluste derartig vergrößert werden, daß dies wiederum zu anderen Nachteilen führen kann.
Inwieweit der Wellenwiderstand bei NF-Übertragungen nun wirklich eine Rolle spielt, ist noch weitgehend ungeklärt. Beim Betrieb eines Lautsprechers an einer üblichen Endstufe treten schon derartig niedrige Impedanzen auf (Lautsprecherbox nominal 8Ω, Endverstärker nominal 0Ω), daß man höchstens nur unter Inkaufnahme großer Leistungsverluste einen Aufbau des Lautsprecherkabels ins Auge fassen könnte, bei dem sich der Wellenwiderstand im NF-Bereich innerhalb der beiden Werten bewegt. Inwieweit dieser Aufwand einem eventuell zu erzielendem Klangvorteil entsprechen würde, vermag niemand vorherzusagen.
Wichtig auf jeden Fall ist die Beachtung des Wellenwiderstandes und des korrekten Abschlusses bei digitalen Übertragungsleitungen, z.B. zwischen CD-Laufwerk und DA-Wandler.
Dort können falsch angepaßte Leitungen, bzw. falsche Leitungen durchaus eine Signalbeeinträchtigung und daraus resultierend u.U. eine Klangverfälschung ergeben.

