Bei der Entwicklung der Rudolph & Braun Primus 1983-1984 spielte wegen der zu erwartenden größeren Abhörlautstärken (das war eines der Entwicklungziele, trotz der Pegellimitierung des Ionenhochtönern) das Resonanzverhalten des ziemlich großen Gehäuses eine Rolle, die es zu untersuchen galt.
Dem Ionenhochtöner mit seiner Hochspannungsröhre und den Klemmelektroden sollte ein möglichst schwingungsarmes Arbeitsfeld geboten werden.
Die Modalanalyse ist hier das gegeignete, aber leider auch sehr aufwendige Mittel.
Unter Modalanalyse hat man allgemein die Charakterisierung des dynamischen Verhaltens eines schwingfähigen Systems mit Hilfe seiner Eigenschwingungen zu verstehen.
Eine Eigenschwingung ist eine globale Systemeigenschaft, die durch die modalen Parameter Eigenfrequenz, Dämpfung und Eigenform beschrieben werden kann.
Aus den modalen Parametern lassen sich nicht nur die Resonanzfrequenzen des Lautsprechergehäuses direkt entnehmen, sondern darüber hinaus bietet die Kenntnis der modalen Parameter, insbesondere der Schwingungsform, die Möglichkeit durch gezielte konstruktive Maßnahmen das Lautsprechergehäuse an den optimalen Stellen zu versteifen. Versuchsablauf:
Versuchsablauf:
Zunächst wird die geometrische Struktur des zu messenden Gehäuses in Form einer einfachen Skizze approximiert. Danach werden in der Skizze Messpunkte markiert. Die zugehörigen Punktkoordinaten werden in der richtigen Richtung in den Rechner eingegeben. Gleichzeitig werden diejenigen Messpunkte mit eingegeben, die durch Krafteinwirkung in den entsprechenden Richtungen mitangeregt werden.
Die Messpunkte werden per Papieraufkleber am Lautsprechergehäuse markiert. Der Beschleunigsaufnehmer wird durch einen Zyanacrylkleber auf der geometrischen der gegenüberliegenden Seitenwand befestigt (driving point).
Durch einen Schlag mit dem Prüfhammer auf den jeweiligen Meßpunkt wird das Gehäuse kurzzeitig angeregt. Das entstehende Antwortsignal ebenso wie das durch einen im Prüfhammer befindlichen Kraftaufnehmer abgenommene Erregungssignal durchlaufen jeweils einen Tiefpass (Grenzfrequenz 500 Hz), bevor sie digitalisiert werden. Jede Erregung wird mehrmals durchgeführt und deren Ergebnis gemittelt. Die gemittelte Impulserregung und -antwort wird per FFT in den Frequenzbereich transformiert. Um die Gültigkeit des Versuchs zu überprüfen, wird nach jeder Messung die Kohärenzfunktion berechnet und zwecks Überprüfung dargestellt. Die gültige Übertragungsfunktion jedes Messpunktes wird nun abgespeichert.
Im Anschluß an die Messungen ist die zur Darstellung der Schwingungsformen erforderliche modale Datenbasis zu erstellen.
Dazu wird zunächst eine Messung ausgewählt, bei der alle auftretenden Resonanzfrequenzen sichtbar sind. Aus diesem experimentell ermittelten Übertragungsfrequenzgang wird durch iterative Rechnungen eine mathematische Funktion berechnet. Diese iterative Rechnung (Newton'sche Näherung) wird solange durchgeführt, bis der auftretende Fehler annähernd Null ist. Anhand der Anzahl der Iterationen dieser Funktion werden alle übrigen gemessenen Übertragungsfunktionen in mathematische Funktionen umgewandelt. Danach kann der Rechner die erforderliche Datenbasis berechnen. Aufgrund dieser Daten können jetzt einzelne Schwingungsformen generiert und dargestellt werden.
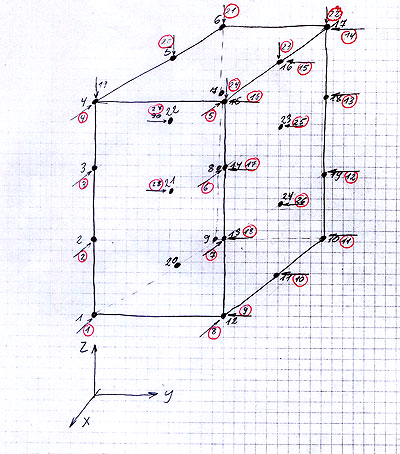
Bild 1. Die geometrische Struktur des Prüflings 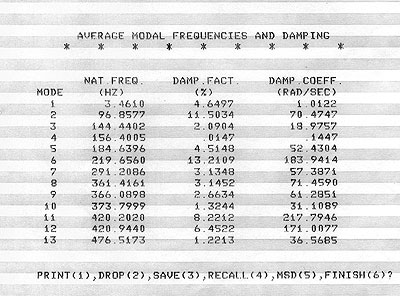
Bild 2. Die gemittelten modalen Parameter
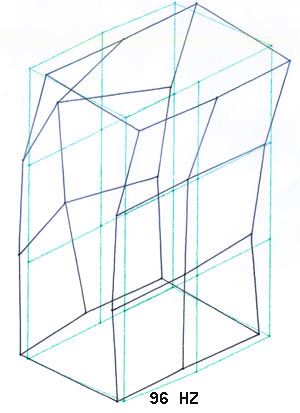
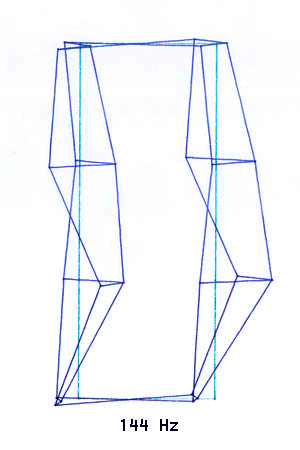
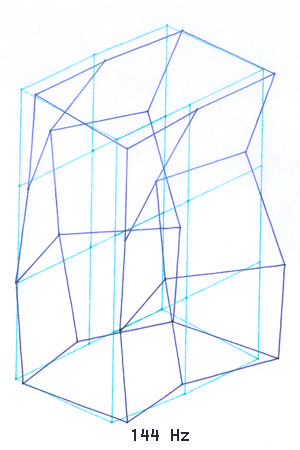
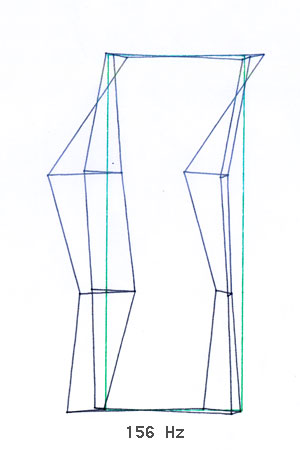
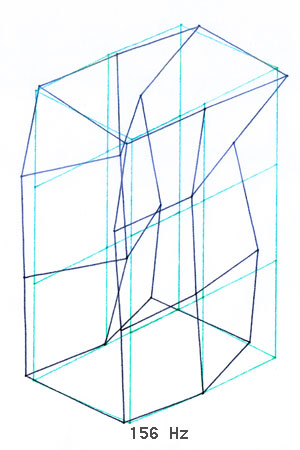
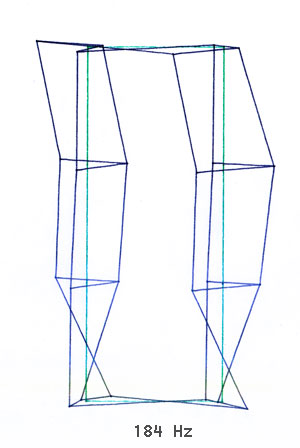
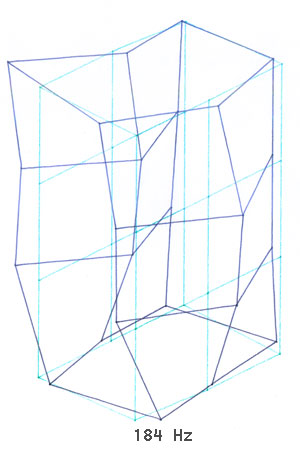
Bild 3-12: Zur Verdeutlichung stark verstärkte Schwingungsformen bei einzelnen Resonanzfrequenzen
Auswertung:
Als Ergebnis erhält man (neben langen Tabellen mit den Rohdaten) eine dynamische Darstellung der Bewegungen aller Meßpunkte bei einer bestimmten Frequenz. Diese Bewegungen (das Schwingen der Messpunkte um ihren Ausgangspunkt) unterscheiden sich in Amplitude und Phase und führen, zwecks besserer Darstellung natürlich extrem stark verstärkt, zu einer sehr komplexen und eindrucksvollen Darstellung.
Bilder 3-12 sind eigentlich nur Standbilder (angehalten bei der maximalen Amplitude) des jeweiligen "Films" des komplexen Schwingungsverhalten bei der jeweiligen Resonanzfrequenz. Dieser "Eiertanz", den das Gehäuse ausführt, sieht schon etwas erschreckend aus und übersteigt in seiner Komplexität schon manchmal das Vorstellungsvermögen.
Wie die Bilder zeigen, ist bei insgesamt nur 28 Meßpunkten (die aber immerhin schon fast 200 Einzelmessungen erfordern) die geometrische Struktur nur sehr grob angenähert. Bei rechtwinklig-kastenförmigen Gebilden ist das aber nicht weiter tragisch. Wichtig ist die Kenntnis der gemittelten modalen Parameter (Bild 2). Da man nebenbei noch Tabellen mit den (relativen) maximalen Amplituden der jeweiligen Messpunkte bei den jeweiligen Resonanzfrequenzen erhält (das hier gezeigte ist nur ein kleiner Teil der Auswertinformationen), kann man sich mit etwas Statistik schnell die relevanten Punkte zur effektivsten Resonanzbedämpfung herausfinden, was ja eigentlich der Sinn der ganzen Sache sein soll.
Anhand der Ergebnisse dieser sehr aufwendigen Meßmethode konnte nun überprüft werden, inwieweit einfachere Meßmethoden wirklich in ähnlicher Weise zielführend waren.
Wie das heute (2011) gemacht werden kann, findet man hier beschrieben.

